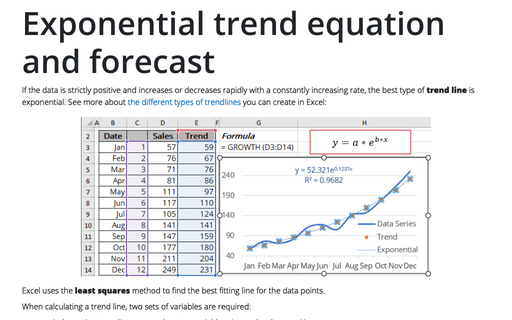
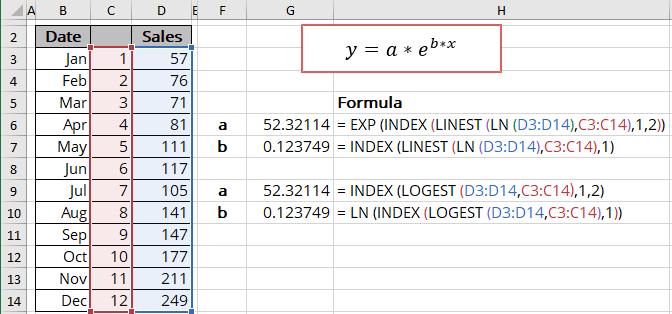
Exponential trend equation and forecast
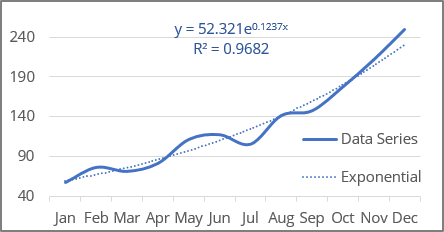
Excel uses the least squares method to find the best fitting line for the data points.
When calculating a trend line, two sets of variables are required:
- an independent, predictor, or explanatory variable x (named as known_x's),
- a dependent or response variable y (named as known_y's).
Exponential trendline equation and formulas
The exponential trendline is a curved line described by the function:
y = a * ebx
where:
- a and b are the parameters of the approximating function (also named function coefficients or constants),
- e is the mathematical constant, the base of the natural logarithm (also known as Euler's number, approximately equal to 2.71828... - the result of EXP (1) - see below the description of this function).
Note: Excel uses a linear model to fit an exponential function: the exponential function y = a * ebx is transformed into a linear function using a change of variables. After changing the variables, the calculations are similar to the linear case Y = b * x + A:
- For a > 0, the variables change to Y = ln (y) and A = ln (a),
- For a < 0 (there is some upper bound c for y), the variables change to Y = ln (c - y) and A = ln (-a).
To find parameter a, it is necessary to perform the inverse transformation a = EXP (A) or EXP (-A).
Excel offers the following functions to calculate the trend parameters:
Using LINEST function:
- a: = EXP (INDEX (LINEST (LN (known_y's), known_x's), 1, 2))
- b: = INDEX (LINEST (LN (known_y's), known_x's), 1)
Using LOGEST function:
- a: = INDEX (LOGEST (known_y's, known_x's), 1, 2))
- b: = LN (INDEX (LOGEST (known_y's, known_x's), 1)
Note: You can use any of these functions to get different parameters. For example:
- a: = INDEX (LOGEST (known_y's, known_x's), 1, 2))
- b: = INDEX (LINEST (LN (known_y's), known_x's), 1)
The EXP () function returns the result of the constant e raised to the power of a number:
= EXP (number)
where:
- number (required) is a power that e is raised to.
The LN () function is the inverse of the EXP () function and returns the natural logarithm of a given number:
= LN (number)
where:
- number (required) is a number to take the natural logarithm of.
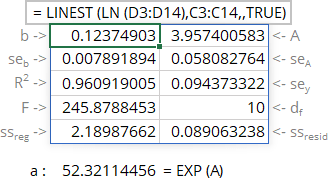
The array function LINEST () calculates the linear trend best fits the known data and then returns an array with statistics describing the trend line:
= LINEST (known_y's, [known_x's], [const], [stats])
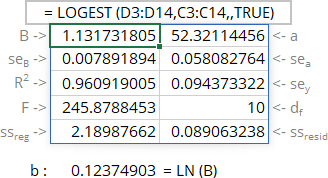
The array function LOGEST () calculates the exponential curve that fits best the known data and then returns an array with statistics describing the trend line:
= LOGEST (known_y's, [known_x's], [const], [stats])
where:
- known_y's (required) are dependent data values,
- known_x's (optional) are independent data values. If known_x's is omitted, it is assumed to be the array {1,2,3,...} that has the same size as known_y's,
- const (optional) is a Boolean value specifying whether to force the parameter a to equal 1 (or A set to 0). Those, the exponential curve would pass through the point (x = 0, y = 1):
- If const is TRUE or omitted, the parameter a is calculated normally,
- If const is FALSE, the parameter a is set to 1, so the function will look like y = ebx.
- stats (optional) is a Boolean value specifying whether to return additional regression statistics:
- If stats is TRUE, the function returns the additional regression statistics in the form of an array:
where:
Line Statistics Description 1 b a Parameters of the function 2 seb sea Standard error of parameters 3 R2 R-squared value sey Standard error of y estimate (also known as Standard Error of a regression) shows how big the prediction error is 4 F F statistic (F-observed value) dr Degrees of freedom 5 ssreg Regression sum of squares (also known as SSR) ssresid Residual sum of squares (also known as SSE) - If stats is FALSE or omitted, the function returns only the calculated parameters.
- If stats is TRUE, the function returns the additional regression statistics in the form of an array:
Notes:
- If you have a version of Microsoft Excel other than Microsoft 365, functions that return arrays must be entered as array functions using Ctrl+Shift+Enter unless you can just press Enter.
- Because the LINEST () and LOGEST () functions return an array of data, you can use the INDEX () function to display only the desired parameter(s) from the returned data array.
- Because the statistics are calculated for the linear model, the statistics array and chart values are different.
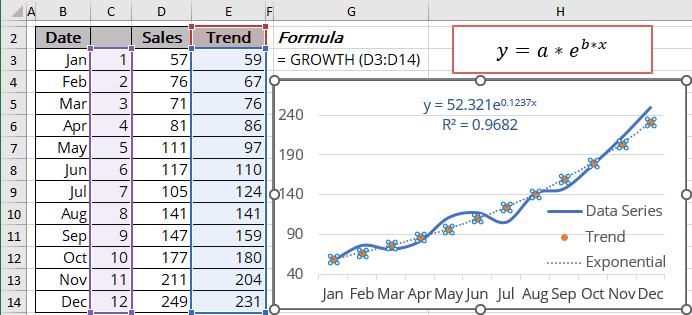
Calculating the exponential trendline values
To calculate the exponential trendline values, Excel offers the array function GROWTH () (see the notes above about array functions) that returns values for the exponential trend:
= GROWTH (known_y's, [known_x's], [new_x's], [const])
where:
- known_y's (required) are dependent data values,
- known_x's (optional) are independent data values. If known_x's is omitted, it is assumed to be the array {1,2,3,...} that has the same size as known_y's,
- new_x's (optional) are the new x-values for which the GROWTH () function should calculate corresponding y-values:
- If you omit new_x's, it is assumed to be the same as known_x's,
- If you omit both known_x's and new_x's, they are assumed to be the array {1,2,3,...} that is the same size as known_y's.
- const (optional) is a Boolean value specifying whether to force the parameter a (intercept) to equal 1. Those, the curved line would pass through the point (x = 0, y = 1):
- If const is TRUE or omitted, the parameter a is calculated normally,
- If const is FALSE, the parameter a is set to 1, so the formula will look like y = ebx.
Note: You can get the same results using the function TREND () as for linear trend:
= EXP (TREND (LN (known_y's)))
R-squared value
The R-squared value calculates for exponential regression in the LINEST () and LOGEST () functions statistics incorrectly because of using the linear model! You can see different values in the statistics array and on the chart.
The R-squared value (in Excel, R2) determines how well the trendline fits the data. The R-squared value can vary from 0 to 1: the nearer R2 is to 1, the better the trendline fits the data.
The R-squared value displayed on the chart (see how to turn on the R-squared value) shows the Pearson correlation. You can easily calculate that value:
- Use the RSQ () function that returns the R-squared value of two data sets:
= RSQ (array1, array2)
where array1 and array2 (both are required) are two data sets:
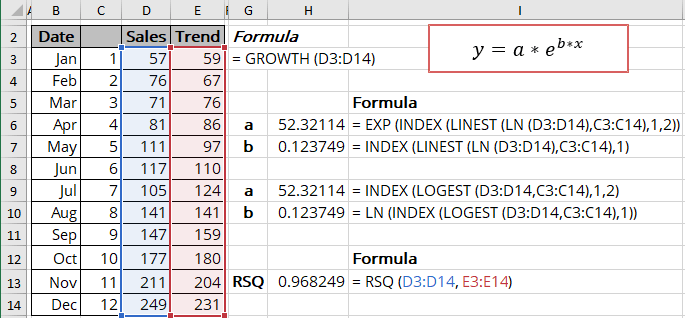
Notes: The value you see in the LINEST () and LOGEST () statistics is the R-squared value between the logarithms of array1 and array2. In this example:

Forecast using the exponential trendline
Using the GROWTH () function, you can calculate the predicted values y for the new_x's:
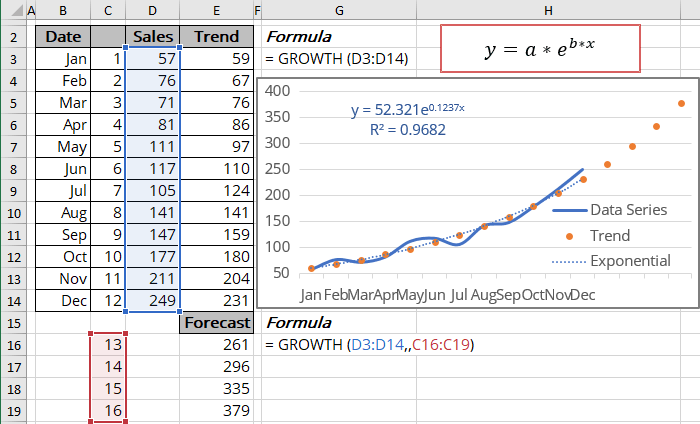
Note: You can get the same results using the function TREND () with the following transformation:
= EXP (TREND (LN (known_y's), , new_x's))